Music Fiction 101
A vs. C — Solution 3:
Only the Names Have Changed (and the natural half steps!)
Solution 3: Transposing all letter names and natural half steps
Here's the best approach for dethroning C and seating A at the top of the Cycle of 5ths.
By lowering each letter name by two letters we make a grand, global musical transposition. Every C become an A, all Ds are renamed B, all Es become Cs, and so on, renaming the piano keyboard like this:
The resulting A scale possesses the qualities and simplicity of the former C scale. To play the A major scale (the scale formerly know as C) start on our new A and play all white keys to the next A.
Because this 'A scale' contains no sharps or flats it is now the simplest scale on the piano, and the simplest scale to notate.
So, what about notation? We must apply the same transposition to the letter names of the grand staff (the Treble clef and Bass clef, lower the name of each line and space by two letter names. This is not as extreme as it sounds. Clefs rename the staff lines all the time. However G, F and C clefs are the only official clefs, so I've proposed and chosen an A clef symbol, and in the day of the Internet, perhaps nothing suits the occasion better than the ubiquitous @ symbol. Also notice, fittingly the piano’s middle C becomes middle A!
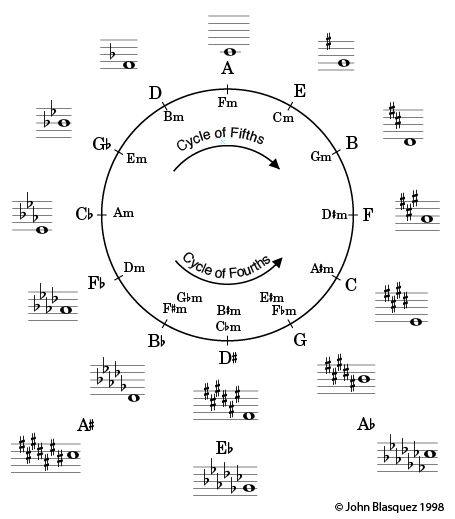
Notice that each key signature in the A-based Cycle of Fifths has a whole note. This note indicates the where the root of the key begins notationally. Sure enough, the whole note in the A key signature is one line below the staff.
Now there’s yet another factor to consider. The natural half-steps. If you look back to our transposed keyboard, you'll see they've been transposed as well. They now fall between C-D and G-A, no longer between B–C and E–F. Fully transposing the staff in this manner changes only one thing: the names of the notes.
Finally an accord is found ... and the result is profound! But what about scale formulas and key signatures???
The new system reads just like all previously used clefs, including key signatures, and accidentals. No music scores need be rewritten. No readjusting of minds — except to remember the new lettering and new key signatures. It's perfectly simple, only the names have changed!
Renaming the staff lines produced a nice bonus. The ledger line that separates the grand staff’s treble and bass clefs (the line formerly known as middle C) is now middle A!
At the crowning ceremony it would only seem fitting that the new "Alpha" clef (A-clef) replace the treble clef (the G-clef). Oh, and we must treble clef is now an E-clef, not a G clef. Sorry G.
Transposing the natural half-steps.
In music, throughout the centuries, C has achieved special status for one probable reason. The C scale has no sharp or flats.
Let’s examine the reasons for this. Why is the key of C is free from sharps and flats? Historical origins aside, it’s because of the position of music’s “natural” half-steps, which fall between B and C and between E and F.
So let’s review our basic knowledge of music theory. The most global musical rules mandate:
• The interval (the musical distance) between letter names is always a whole-step, with two exceptions: There is a half-step between B and C, and between E and F. These two exceptions are called “natural” half-steps. Because they occur between letter names (B natural and C natural, or E natural and F natural), no sharps or flats required. When you move a half step from any other letter name, you move from a natural name to a sharp or flat ... or you move from a sharp or flat to a natural name. In other words, an accidental is always involved, either in the name of the initial note or the name of the destination note.
• Keys and key signatures are defined by the formula of the major scale. The formula for the major scale is W W h W W W h, where 'W' stands for a whole step and 'h' stands for a half step. A sequence of notes played according to this set of intervals produces the familiar solfegio sound: Do, Re, Mi, Fa Sol, La, Ti, Do, and is numerically represented with; 1,2,3,4,5,6,7, with a half step between 3-4 and 7-1.
So it follows, if the half-steps now fall between C-D and G-A then the scale A, B, C, D, E, F, G is a major scale. It fulfills the formula WW h WWW h and produces the solfegio Do, re, mi. The key of A, instead of having 3 sharps, now has none. The A scale requires no sharps or flats, so it earn the position at the top of the Cycle of Fifths.
Accordingly, the key of F has three sharps. Let's think it through to see why.
Whole-step: F to G is a whole step.
Whole-step: We need another whole-step, but G to A is a half-step, so we need G#.
Half-step: G# to A is a half step.
Whole-step: B to C is a whole step (remember?).
Whole-step: C to D is a half-step, so we need D#
Whole-step: D# to E is a half-step, so we need E#
Half-step: E# to F is a half-step
So the resulting scale is: F, G#, A, B, C, D#, E#. Three sharps! And the three sharps remain in the same place on the staff. (And a treble clef, is now an E clef, no longer a G clef!)
The two-letter transpositional lowering applies at every level. The 'old school' key of A had three sharps: F#, C# and G#. F (two letter names lower) is new key with three sharps , and those sharps are D#, E# and G#, each two letter names lower than the chromatics in the key of A.
Each key's position on the cycle of 5ths is determined by the number of sharps in the key signature. Thus F's position on the Cycle of Fifths is in the location of the former key with three sharps.
I know, I know ... it's a bit like calculating dollars to Euros in base 7.
Our global transposition resolves the constant friction between A and C and rightly makes A the alpha of music theory and music notation.
If you understood this, then you truly understand music theory, because it's all about relationships.
Pros:
• Many
Cons:
• None, except the natural resistance to change, even when logic prevails
Music Fiction | TheoreticallyCorrect.com | Singingwood Music


