A musical slide ruler

for determining the letter names

of major scales and chords

Introduction

If you're interested in understanding the basics of music theory and the nuances of music grammar you'll need to know how to correctly "spell" the various major scales. The resources on this page should help you learn to do so.

With the interactive musical slider ruler provided here, and the discussions below, you'll be able determine the letter names of the notes of any major scale. So let's take a detailed look at the major scale, and how to use this slide ruler above.

Major scale = Do, re, mi ...

All major scales produces the sound of "do, re mi ..." In other words, they all conform to the the same formula— they share the same pattern of intervals between notes.

The formula for a major scale

The formula for a major scale is:  W  W  1/2  W  W  W  1/2 

• W means a whole step (the distance of two notes, or two frets)
• 1/2 means a half step (the distance of a single note, or one fret)

Scala profundo! The major scale is the cornerstone of western music theory and clef based music notation.

The major scale formula is the core defining structure throughout western music theory. All chords and scales reference the major scale, and are defined in relation to it. In other words, their formulas are some sort of variation or deviation from the major scale formula.

The intervals of the major scale formula determine letter spelling of the fifteen major scales in common usage. These share the same formula, and simply have different roots—and they are the basis for the fifteen keys. Glossary note: The root is the starting point of the scale, aka the letter name of the scale, such as: A or Bb, B, C, C# ...

Key signatures

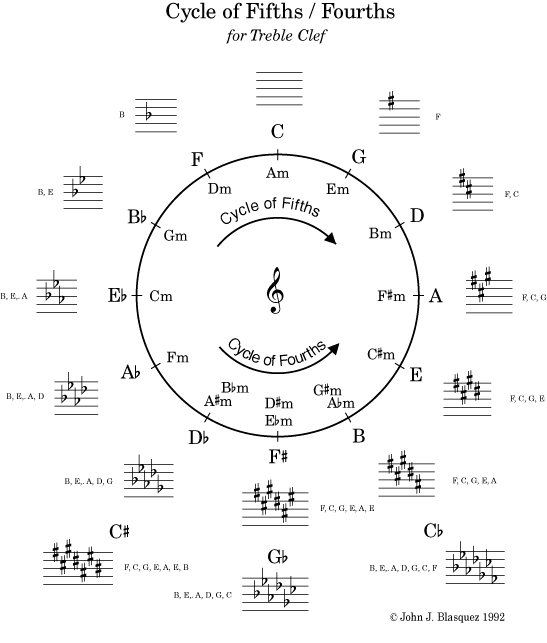
Regarding its impact on music notation, the major scale's formula defines the fifteen pragmatic key signatures found on the Cycle of 5ths.

You can start a major scale on any note. The starting note is referred to as the "root" or "name" of the major scale. The commonly accepted notes are A, Bb, B, C, C#/Db, D, Eb, E, F, F#/Gb, G, G#/Ab.

About the slide ruler

The slide ruler illustrates and illuminates the basic concepts of scale construction and scale degree naming. However, as with all simple musical slide rulers, the correct answer is not a simple "lookup".

When there are two possible names for a note (i.e. enharmonics) you must make a grammatical decision. The rules for choosing the correct name are explained below. (Glossary note: An enharmonic is a musical synonym—an alternate name for the same sound, whether a note, chord, mode. For instance F# is enharmonic for Gb—both names refer to the same pitch. A D6 chord and a Bm7/D chord are enharmonic because they contain exactly the same notes. There are rules of grammar and notation that usually determine which "pronuciation" is correct, but sometimes it's up for debate.

Pros and Cons to slide ruler use

Before proceeding, it bears mentioning. There are pros and cons to using a slide ruler. If it illuminates your understanding to a point where you no longer need rely on it, it has served its purpose well. Nevertheless a musical slide rule is handy when you're stuck or not feeling 100% sharp. And it can be a vital resource for anyone learning about music. But, as mentioned, most slide musical slide rulers require some level of interpretation; without interpretation they produce incorrect or grammatically marred information. So be mindful when using one, and be ware of the various edges where answers may fray into grammatical disarray.

For anyone interested in exploring beyond the major scale, you'll find an extensive listing of chord formulas and scale formulas at Sound Thinking—an interactive chord and scale encyclopedia for stringed instruments. You can use Sound Thinking to display dozens of correctly spelled chords and scales, in any key. Additionally it helps people visualize and explore the chords and scales on stringed instrument.

Using the Slide Ruler on this page

The slide ruler on this page initially displays the C major scale:

      C D E F G A B

Arrows point upward from each scale degree (1st, 2nd 3rd, etc.) to the corresponding letter names (C, D, E ...) In other words, the 1st degree of the C scale is C, the 2nd degree is D, the 3rd degree is E ...

C is the simplest scale to spell, as you can see, because it has no sharps or flats. All other scales with have at least one sharp or one flat.

Slide Ruler Controls

• Click slide ruler's right and left arrows to slide the tan colored strip sideways. This allows you to move any letter into the root position, above the 1st degree.
• Alternately you can drag the strip of letter names into the desired position.
• When you align D with the number 1, the arrows will point to:

        D E F# G A B C#

• Note that the D major scale is spelled using F# and C# rather than Gb and Db. The reason for this is explained below.

Note naming / Resolving enharmonics with the slide ruler

Although the slide ruler affords all the necessary information, in order to correctly "spell" the scale according to the rules of musical grammar you'll usually need to make some decisions. The C Major scale is the only scale that contains no sharps or flats. You'll see that the other modes of the C major scale, such as the A minor scale, also have no sharps for flats.

When you have the choice of a sharp name or a flat name (for instance, A#/Bb,  C#/Db,  D#,Eb,  F#/Gb,  G#/Ab), the general rules are:

• If the root is F, or if the root includes a flat, such as Bb, Eb etc., always choose the flat name. In other words, the key of F or anything that's counter-clockwise from F on the Circle of Fifths.
• Otherwise use the the sharp name. This applies to the key of C and any key that contains a sharp in the key signature. In other words, the key of C or anything that's clockwise from F on the Circle of Fifths.

This slide ruler is a tool that affords the answer for you, but it's wise to understand why these answers are correct. The following section will explain why.

Musical principles to bear in mind

If you are new to music, music notation, and music theory, you'll need to grapple with some basic concepts:

• The music language uses just seven letter names to represent the full range of music notes. These names are used successively. It's like counting the days of successive weeks like this:

  1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3...

• There are numbering systems such as the Helmholtz Pitch Numbering System that identify the various ranges of C to C, but musicians usually communicate clearly by letter name alone, without the need to identify the range.
• Consecutive musical notes are recognized and organized in groups, as bunches of twelve. (There are perceptual and scientific reasons for this, but for now it is only important to understand that this is true.)
• The bunches of twelve are called octaves. In other words there are twelve musical notes notes within each octave. The thirteenth note IS the octave. (Which begs the question, "What does eight have to do with thirteen?"

• With in each octave only seven of these twelve notes have letter names. These are called natural notes, because they require no sharp or flat.
• The other five notes have no name of their own, and must borrow a letter name from a neighboring note. These are called enharmonic notes.
• There is a note between all letter names, except between B to C and E to F.
• A preponderance of European and early classical melodies usually use only seven of the twelve notes, in the same manner in all octaves. Undoubted this led to the naming of only seven notes— the musicians of the day were only interested in naming the notes they used frequently.
• A melody or scale may span a number of octaves.

Here's an example of enharmonic note naming.

There is a note between F and G, but it has no letter name of it's own. The possible names are F# or Gb. Out of context either name will identify the pitch of the note. But in the context of a key, scale or chord, when confronted with an enharmonic choice like "F#"verses "Gb" you must decide which letter name to choose.

You'll can always determine correct answer if you consider the degree of the scale. If the degree of the scale is a 6th, then you must choose the letter that is the 6th letter of the scale. Simple as that.

Here are two examples:

• The letter name of the 6th degree of the E scale is C. So when deciding between C# and Db you cannot choose Db, because D is the letter name of the 7th degree of the scale.
• The D major scale is properly spelled: D E F# G A B C# ... not D E Gb G A B Db. Granted, two spellings identify the same sounds, but in the context of a particular scale or key, only one spelling is correct. In the D scale the 3rd degree must be an F# not a Gb. The 7th degree must be a C# not a Db.

Chord Formulas

You can use this slide ruler to spell the notes of any triad (major, minor, augmented or diminished) or dominant 7th chord (major 7, minor7, dominant 7 or diminished 7). You simply need to know the formulas for chord formulas.

The formula for a major chord is 1, 3, 5, therefore

a C major chord is C E G
a D major chord is D F# A
...

The formula for a minor chord is 1, b3, 5, therefore:

a C major chord is C Eb G
a D major chord is D F  A
...

The formula for a dominant 7 chord is 1, 3, 5, b7, therefore:

a C7 chord is C Eb G Bb
a D7 chord is D F  A C
...

Resources for chord and scale formulas

Sound Thinking contains an extensive list of chord formulas and scale formulas.

More information about transposing at Key Switch

Limitations of Musical Slide Rulers and "Wheels"

While a physical musical slide ruler can provide lots of answers, inevitably it will require some attention and decision making on your part. Slide rulers also allow choices you "shouldn't" make, such as choosing A# for the root of a key; while the key of A# is theoretically viable, and it's covered in the Spiral of 5ths, it is not a member of the Cycle of 5ths because it is not a normal key signature used in music notation—the reason for its exclusion is that it has double sharps in the key signature,and there's always a simpler alternative; in this case Bb.

Furthermore, a simple slide ruler cannot be entirely accurate. In the case of A#, this slide ruler does not show F##, C##, and G##. One could argue this is a moot point because, as mentioned, you should choose A# for the root of a scale. However, A# maybe an legitimate root for a chord! But these types of rulers will not help you spell chords with "out of gamut" roots like A#.

In the future I'll create another slide ruler that intelligently shows the correct letters names for any scale or chord. Part of the purpose here is to demonstrate that the limitations that all musical slide rulers share. (Read more ..."

For detailed information about scale formulas, chord formulas and the correct spelling of those in any key, see Sound Thinking.

Cycle of 5ths